Jiri Brezina

ABSTRACT:  Sedimentation velocity of a single grain is the most accurate measure of grain size. The advanced settling tube system extends this accuracy to particle collectives and thus provides a powerful tool for sand sedimentology. The author's advanced settling tube system, MacroGranometer™, adds operational and maintenance ease, and variety of results.

ADVANTAGE of SAND-SIZED over FINE PARTICLE SIZE DISTRIBUTION

Distributions of fine particles obeying Stokes', i.e. viscous, sedimentation (Reynolds' number Re <0.1) does not allow much sedimentological interpretation for the following reasons:

1. The fine particles sediment very slowly in nature thus being part of the fluid medium (environment) without influencing their size distribution;
2. The sedimentation of fine particles in nature could be influenced by properties caused by their great specific surface such as electrical charge leading to a selective coagulation; the distribution properties become erratic;
3. The size of fine particles could change by post-depositional processes, such as compaction, cementation and re-crystallization.

Sand-sized particles, in contrast, are sensitive to source and transportation influences. Therefore, the size and sedimentation velocity distributions of sand-sized particles do reflect the source and transportation influences.

ADVANTAGE of SEDIMENTATION for SIZE DETERMINATION over Sieving and other Methods

The size of a single grain can be determined most accurately by its sedimentation velocity, controlled by mass, volume and shape of the grain. Sieve and optical measures are one-level dimensions. 

Non-sphericity, particularly flatness, decreases the sedimentation size but increases the sieve size. This is why flatness causes that the specific surface and related properties are calculated from sieving as smaller, instead of as being larger when derived from sedimentation. Therefore, the sedimentational grain size is influenced by grain shape consistent with the grain specific surface. Whereas other settling tubes are using sedimentation formulas for spherical grains only, the author's MacroGranometer™ is based on the author's formulas, which enable to choose a more realistic particle shape (SF = 0.65 is standard).

Settling rate of a coarse irregular grain is invariably given, as the non-viscous drag of water keeps it in a defined position. Sieve results include random error due to changing grain position, limited grain access to sieve holes, their blocking, large sieve intervals etc.. Thus sieving requires large samples to "absorb" the random error and to provide a sufficient sample representatives. Nevertheless, from non-sedimentation methods, precision wet sieving using circular holes and a sieving time proportional to the grain number per hole of each sieve provides the best standard definition of a geometric grain size.

The sedimentation grain size is surely the "natural" quantity related to the origin of sediments and sedimentary rocks. However, sedimentary origin is no excuse for analysis distortions by ordinary settling tubes. These distortions do not mimic natural processes but seriously mask the proper ones to be found and quantified by sedimentological interpretation. Until today, the paraphrase of W. Shakespeare by R. L. Folk (1962) is valid: "The fault, dear Friends, lies not in the sands, but in your tubes, that they are skewing things."
The sedimentation velocity, together with the geometric grain size, allows the determination of the grain density or shape, even in distributions.

SETTLING TUBES are BASED on STRATIFIED SEDIMENTATION J. Brezina, 1979 (PARTEC 44 A5 pdf pages to view & download)

Advantage of Stratified Over Homogeneous Sedimentation

In groups, particles must be allowed to sediment at mutual distances such that their settling velocities become close to those of single particles. Sedimentation of coarse (sand-sized) grains in water generates forces which liberate the grains from each other: these forces surpass the water viscosity as the particle Reynol ds' number is greater than about 0.1. Therefore, the group of coarse grains does not need to be homogenized for sedimentation, but can be introduced at the top of a particle-free fluid. Particles become distributed vertically according to their settling velocity, which is identical for particles in each level: so called stratified suspension (H. J. Skidmore, 1948, ref. 69; John S. McNown and Pin-Nam Lin, 1952, ref. 67) develops, and stratified sedimentation takes place.

Stratified sedimentation enjoys a fundamental accuracy advantage over homogeneous sedimentation. First, the sedimentation length of all particles is known in a stratified suspension. In homogeneous suspension, the sedimentation length is known only for the topmost particles at the beginning of sedimentation; other particles interfere with them and their weight must be eliminated mathematically by taking a derivative. Secondly, the particle concentration (and thus the particle interference) rapidly decreases in expanding volume of stratified suspension, but it increases in the shrinking volume of homogeneous suspension.

This advantage of a stratified sedimentation of sand-sized particles, together with speed and price, explains the success of ordinary settling tubes, although some of them, such as the Emery's settling tube (Kenneth O. Emery, 1938, ref. 64), are exceedingly primitive.

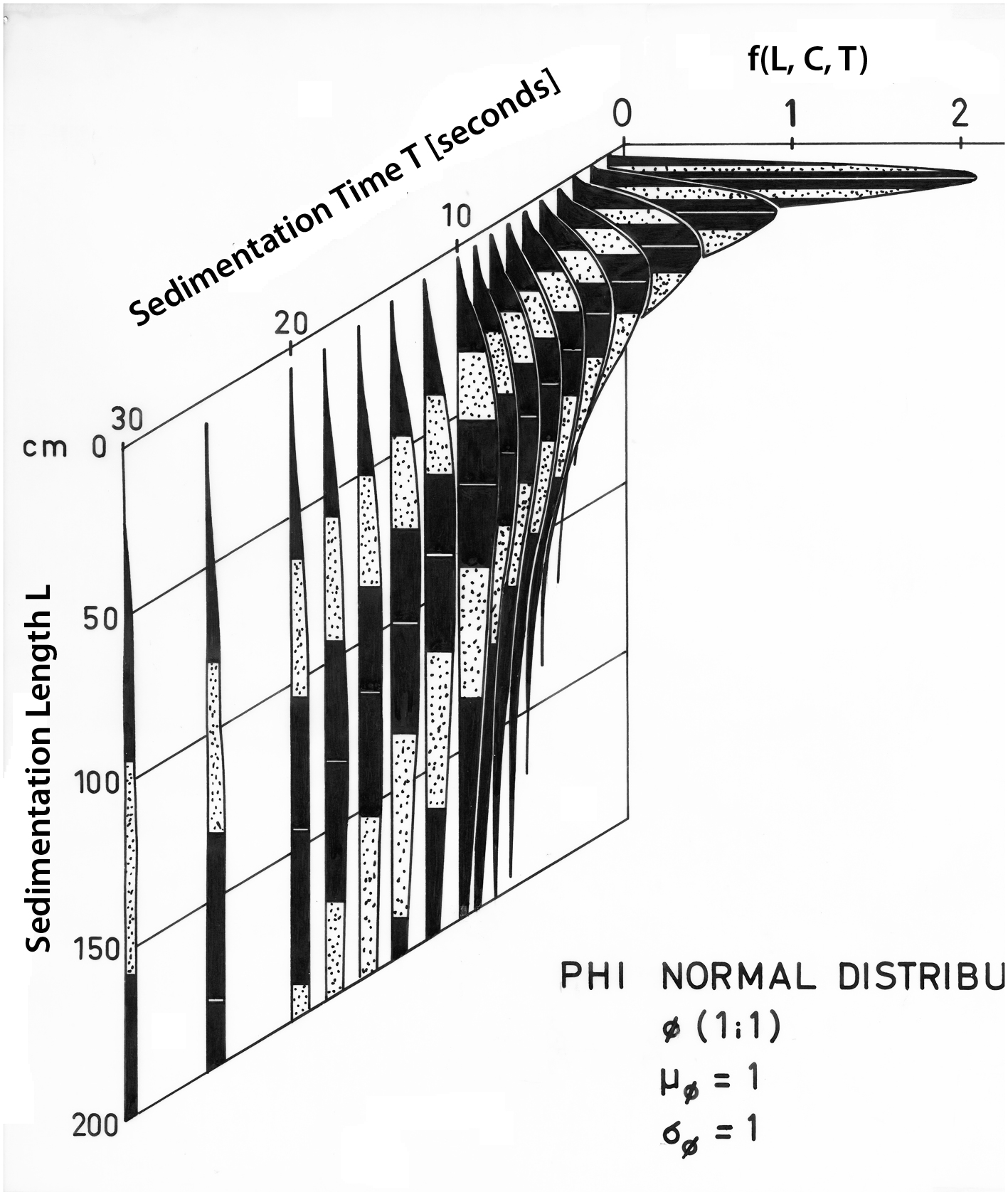
Theoretical Stratified Sedimentation

A theoretical settling rate frequency distribution during stratified sedimentation of a sand is shown in a three-dimensional diagram (Fig. 1, J. Brezina, 1970, ref. 41). The sand has a normal phi (Ø) -size distribution with both the mean size and the standard deviation equal to 1 Ø, written in the standard format Ø (m, σ). The two parameters of the normal distribution m = mean and σ = standard deviation are both one, in the given case Ø (1, 1). The vertical axis is the sedimentation length L, the horizontal axis shows the frequency which is proportional to particle concentration and suspension density. The diagonal axis is sedimentation time T so that the sedimentation length at each sedimentation time instant corresponds to the sedimentation velocity. After the sand is released to sedimentation, its sedimentation velocity distribution is shown at various sedimentation time instants.

Hydrodynamic Instability in a Stratified Suspension

The suspension density is strongest at the top when the sample is released: this is why a stratified suspension sedimenting in a clean fluid is hydrodynamically unstable at the beginning. Its lower portion up to its center with the maximum grain concentration has a negative density gradient, i.e., each overlaying layer has a higher density than the layer (or clean fluid) below, until the maximum concentration layer has settled (Fig. 1). The upper heavy fluid overlaying a light fluid, may form density convection. Due to the continuity principle, rising currents of lighter fluid replace the same volume of the sinking heavier suspension. Various types of density streaming due to hydrodynamic instability (known as Rayleigh-Taylor and Kelvin-Helmholtz instabilities, CHANDRASEKHAR, 1961) have been studied using mathematical models in the Los Alamos Scientific Laboratory, New Mexico (Bart J. DALY & William E. PRACHT, 1968; Bart J. DALY 1967, 1969; R. E. DUFF, Francis H. HARLOW & C. W. HIRT, 1962).

Ordinary Settling Tubes coarsen, diffuse, positively skew etc. the PSI and PHI distributions

A low sensitivity of sedimentation sensors of ordinary settling tubes requires too high particle concentration, producing serious distortions which can hardly be estimated and compensated for, since they also depend on the unknown sample. Specifically, these distortions damage the reputation of the theoretically perfect stratified sedimentation mainly in three ways:

1. The mean size becomes coarser;
2. The standard deviation becomes greater;
3. A positive PSI-sedimentation velocity (and PHI-size) distribution asymmetry (skewness) forms: it either reduces or cancels the negative one, or replaces the zero asymmetry.

Large samples (introduced without any homogenization) disturb the stratified suspension by causing strong streaming with periodic expansion and slowing down. The bottom of the suspension cloud expands downwards in proportion to the density gradient which first decreases due to mixing with water and later increases from particles accumulating on the bottom of the suspension cloud. The following stages of the expanding cloud develop as a rule:

1. The bottom of the suspension expands downwards and accelerates.
2. Mixing with water reduces progressively the suspension density and thus its accelerated streaming.
3. The fastest particles within the suspension cloud catch up with the retarding bottom of the cloud and concentrate there: a bottom front forms.
4. The growing suspension density at the front exceeds a limiting value: the front breaks.
5. Stages 1 and 2 occur; stages 3 and 4 continue only if the particle concentration is still too high: then a full cycle may develop.

Narrow settling tubes (with a diameter less than 15 cm) may reduce the streaming of large samples (coarse particles), but wall effects delay some particles making the distortions more complex.

Advanced Settling Tube System - MacroGranometer™

The Advanced Settling Tube System virtually eliminates the distortions of the ordinary settling tubes. It approaches the highest theoretical accuracy of sedimentation of sand-sized particles in water.

The advanced settling tubes surpass all other methods of size distribution analysis, such as:

• image analysis,
• laser diffractometry,
• particle counting by resistance pulses,
• laser pulses,
• light blockage, etc.;
• the ordinary settling tubes, which use:
  • sediment volume sensing,
  • manometric suspension sensing,
  • photometric suspension sensing,
  • gravimetric sediment sensing using a sample introduction without dispersion (such as that by vibration of a Venetian blind lamellae), and a weighing pan suspended from an ordinary analytical balance.

Only the advanced settling tubes feature the high resolution sediment weighing combined with a high resolution PSI-sedimentation velocity (PHI-grain size) resolution. Only the advanced settling tube system enables that the classical sedimentological interpretations become reliable and new solutions are possible. They make the efforts meaningful.

The effectivity and importance of the features listed below have been tested and confirmed on various MacroGranometer™ versions - the author's Advanced Settling Tube System.

The author calls his product MacroGranometer™, a size analyzer of coarse grains, in contrast to his early MicroGranometer™, a size analyzer of fine particles. Both instruments take advantage of the stratified sedimentation. Whereas the sedimentation of sand-sized particles can be maintained stable by using the smallest sample size, the sedimentation of finer particles is much more affected by sample size: a maximum of 20,000 particles finer than 50 µm would require only microgram sample size (see below). Therefore, the author's MicroGranometer™ stabilized the stratified sedimentation by a density gradient technique. The instrument permitted to analyze up to seven samples simultaneously. However, although the author was successful in the instrument design, he still discontinued a further MicroGranometer™ development because of the unreliable sedimentological interpretation even of the best distribution analyses of fine particles.

Instead, the author has focused his efforts onto the research and development of the MacroGranometer™, the sand sedimentation analyzer, in all related fields, such as mathematical statistics (theory of distributions), hydro-mechanics of sedimentation, mechanical engineering, instrument construction, and system analysis for computer solutions for three decades. Constructional (CAD), electronic and software solutions have been accomplished in cooperation with professionals.

The author has developed a series of hardware and software solutions in order to make particle concentration low enough and so keep the streaming influence negligible. From his studies on streaming in stratified suspensions, J. Brezina, 1970b (ref. 43) determined that the particles do not influence (drag down) each other when they are at a mutual distance greater than 3.5 mm, which means a limiting concentration of about 0.07% corresponding to suspension density 1.0012 (for 0.2 to 0.5 mm particles).

In addition to the particle concentration lowering, the author (J. Brezina, 1971b, ref. 43) suggested using a positively stratified fluid, i.e. with a positive vertical density gradient (lighter fluid above the heavier one) to avoid the hydrodynamic instability. He calculated a temperature distribution for the top of water column to compensate for the opposite density gradient of a stratified suspension when using various sample sizes. The author suggested an efficient streaming compensation: a slight heating of the top of the water column in most critical cases, i.e. when small samples of fine material are used. Temperature increase by a few degrees Celsius in the top few centimeters of the sedimentation column reduces or eliminates a low concentration streaming in the MacroGranometer™.

Reaching The Lowest Particle Concentration

Three solution groups reduce the particle concentration sufficiently:

1. Highest weighing resolution of the underwater balance to sense the smallest samples.
2. Expanding the sedimentation column diameter. This increases the balance pan diameter, which slows the weighing, thereby reducing the sedimentation time (and particle size) resolution. Therefore, the response of the underwater balance must be made as fast as possible (see the next chapter).
3. Homogenization of the initial suspension top to decrease the highest (initial) particle concentration. For this purpose, a special Venetian blind with vibrating lamellae has been developed.

A. Smallest samples.

The smallest sample size is limited by the sample representatives (about 15,000 to 20,000 grains, J. Brezina 1971b, ref. 43).

Suspension sensing, such as by pressure (piezometric or manometric methods, e.g. Woods Hole Rapid Sediment Analyzer), was tested, but rejected. Attempting to increase the accuracy by reducing the particle concentration decreases the measurement sensitivity. This handicap can not be compensated for by any advantage the suspension sensing offers, such as operational ease (sediment does not need to be removed) and low price.

This is why a sediment sensing (by weight) must be used. The author developed a compact underwater spring balance. The spring arrangement eliminates an asymmetric load moment (German patent 2,251,838 by J. Brezina, 1972b, ref. 46), its load displacement is extremely small: 0.1 mm per 10 gram of quartz underwater weight. Therefore, it is not only very sensitive (10 µg at a measuring range for 0.1 g quartz sample means a resolution of 0.01%) but also fast and robust (not vulnerable by handling).

The maximum significant sensitivity has been reached by:

1. Weighing sensor: specially designed differential transducer (5 kHz carrier frequency) with the highest coil density, magnetic isotropy along the displacement direction and a differential compensation of the displacement non-linearity. The sensitivity has further been enhanced by choosing the material of the moving core with increased magnetic permeability.
2. Amplification of the underwater balance signal by top quality digital carrier frequency measuring amplifier.
3. Noise reduction has been obtained by:
   1. Mechanical insulation from environmental shock & vibration: high quality air shock absorbers (used for holography) cushion the sedimentation column;
   2. Rigid (not resonating) all parts of the sedimentation column. The slightest vibration of any part of the column and joined tubing would lead to vertical vibration of the water column sensed by the balance:
      1. Modules of boron-silicate glass with a minimum wall thickness of 0.8 cm have been used (instead of acrylic glass columns of ordinary settling tubes).
      2. Venetian blind, the sample introduction device,  is constructed from acrylic glass 3 cm thick.
      3. Any air contact with the sedimentation water is eliminated, especially above the Venetian blind laminae (here the water surface is closed by 1.5 cm thick acrylic glass disc).
      4. Bubble-free water inside the sedimentation column. A free water surface could have waves causing water vibration. Bubbles larger than a few cubic centimeters are elastic, easily compressible and would amplify their resonance frequencies from environmental vibration.
      5. Rigid closings of the glass tube openings are made from acrylic glass disks 3 cm thick.
      6. All plastic tube connections to the sedimentation column are eliminated (such as that for water filling and sediment release from the bottom), because they would act as sound sensors (microphones).
      7. Rigid balance pan: a flat cone with its base on top (diameter 26 cm, height 0.8 cm). Full material with maximum strength but minimum mass and volume is best, such as acrylic glass.
      8. Rigid dumping disk closely below the balance pan: it absorbs the medium frequency vertical vibration of the water column.
   3. The necessary cable bridging over the space from the sedimentation column (cushioned on the air shock absorbers) to the laboratory wall (possible source of environmental vibration) is made at the point nearest to the the sedimentation column suspension (on top). Also, all cables are loose (not stretched).
   4. Data averaging per variable measuring time interval corresponding to 0.02 PSI; the balance output is digitized (16-bit resolution) every millisecond, averaged per 0.02 PSI settling time interval and recorded. Up to 401 balance output values can be recorded between -5.00 to +3.00 PSI values at 0.02-PSI intervals. The variable time interval doubles at each next integer PSI unit:

   Number of measurements (and milliseconds) per time interval;
   the time interval corresponds to the 0.02 PSI increments
   (180 cm sedimentation length)

   n	PSI	PSI + 0.02
   78	-5.00	-4.98
   157	-4.00	-3.98
   314	-3.00	-2.98
   628	-2.00	-1.98
   1,256	-1.00	-0.98
   2,513	0.00	0.02
   5,026	1.00	1.02
   10,051	2.00	2.02
   20,102	3.00	3.02

   5. Analyzing and merging sub-samples; a sample may be split into sub-samples and each analyzed separately; the sub-sample weight proportions are automatically considered in calculating the total sample (mean) analysis.

B. Sedimentation column diameter

Whereas the sedimentation column diameter must as large as possible to allow space for the smallest particles concentration, it must be smaller than the balance pan, leaving about 3 cm sediment-free margin on it (see the particle trajectories above it on Fig. 3).

Because the balance pan with a diameter greater than 26 cm seriously slows the fast balance pan displacement, the sedimentation column diameter must be 20 cm.

C. Reduction of the initial grain concentration on the sedimentation column top

The maximum grain concentration occurs at the beginning of the stratified sedimentation. Its influence can be minimized by homogenization of the suspension during sample introduction. The author's Venetian blind generates about 1 cm thick suspension layer, and releases all particles. The concave lamellae rotate eccentrically (Fig. 2). The concavity radius is greater than the rotation radius: this is why the water inertia stream is focused onto the particles on each lamella and flushes them away. The lamellae keep vibrating in open (vertical) position until all particles pass them (about 3 seconds for finest particles to pass the 5 mm water layer above the lamellae).

Influence of environmental temperature change is reduced by the heat insulation and thickness of the sedimentation column.

Increased Speed of the Underwater Balance

A) Geometry and material of the moving parts of the underwater balance:

1 Reduction of the inertia by minimizing mass of the balance moving parts. The mass of the steel parts including one half of one pair double cross-leaf springs is 34.6 grams, the acrylic glass parts including the balance pan is 210.0 grams; the total mass of the moving parts is 244.6 grams. This is less than one quarter of the values for balances in the best other settling tubes.

2. Reduction of water inertia by minimizing cross-sectional area perpendicular to the load displacement: the balance pan occupies most the area. The pan diameter must exceed that of the suspension column by about 6 cm in order to catch all particles since their trajectories diverge few centimeters above the balance pan (Fig. 3). Therefore, the pan diameter seriously limits the column diameter. Extremely fast balance response (130 milliseconds for 90% of 1 gram load) makes the pan diameter of 26 cm (and thus the column diameter of 20 cm) possible. A larger pan diameter (and broader columns) would delay the weighing response and thus bias the particle size distribution.

B) Rapid measuring response of the electronics system (no weighing compensation by a feed back [compensation] method).

C) Sedimentation length: 180 cm matches the overall system accuracy.

System Modularity

The construction of MacroGranometer™ is such that the client can repair or replace most defective parts himself. The hardware and software components feature modularity making the following operations easy:

• 1. Maintenance (cleaning and on-site repair);
• 2. Repair of defective parts, if necessary, by replacement of whole modules;
• 3. Installation of repaired or upgraded parts.

A) Mechanical modules. Partial disassembly allows for a thorough cleaning and small repairs by client. A complete disassembly, performed by a medium skilled technician guided remotely by GranoMetry per telephone, fax, etc., allows for efficient maintenance, identification of the malfunction and defective part to be repaired, adjusted or sent to GranoMetry in special luggage. The major modules (and two covers of the sedimentation tube) are mutually connected by easily removable screws, and tighten against water leaks by PTFE (Teflon™) gaskets, so that each module can easily be detached:

• 1. Two Glass Modules.
• 2. Venetian Blind
• 3. Underwater Balance

B) Electronic module can be checked for functionality (fuses, power supply, carrier frequency measuring amplifier). Either the whole Electronic Module or its selected parts (power supply, carrier frequency measuring amplifier, or our printed circuit board) can be sent to GranoMetry for repair or exchange in a special luggage.

C) MacroGranometer™ Software for your DOS Personal Computer system. Typical solutions of problems include diagnosis and therapy.

• Context sensitive Help (F1 key)
• Operation Manual
• Re-installation of the GRM™ or SedVar™ software from:
  • Your back-up diskette;
  • Obtained new or upgraded from GranoMetry via email, or on a diskette
• Call, e-mail or fax  to GranoMetry

1. Operation Software, GRM™

The GRM™ software controls the whole instrument operation. Together with the analysis results, the operator can record sample and analysis data. Other important data are recorded automatically, such as date, time, temperature on top and bottom of the sedimentation column, local gravity acceleration, and the GRM™ program version.

The measured analysis data is generated in our Standard Data File Format, presenting the optimum scheme for collecting of the maximum measured amount of data with minimum storage requirements: the PSI-logarithmic sedimentation velocity with a constant interval of 0.02 PSI was chosen as a universal mathematical interface for a flexible data processing.

Easy Operation, Variety of Results

2. Data Processing Software, SedVar™

Because the measured PSI sedimentation velocity distributions are valid for the laboratory terms only (fluid's viscosity and distilled water, temperature, and gravity acceleration), the MacroGranometer's^™ data processing software SedVar™ converts these measured laboratory PSI-sedimentation velocity distributions into those of the following variables:

• standard PSI sedimentation velocity, valid under standard physical terms: distilled water at 24°C, gravity acceleration 980.665 gal
• local PSI sedimentation velocity, valid under local physical terms (fluid's viscosity and density, obtained either from temperature of distilled water, or from temperature and salinity of sea water, and gravity acceleration)
• PHI grain size, specified by grain's shape (Corey's shape factor, SF), valid for constant grain density and shape;
• logarithmic Reynolds' number, valid either for constant grain density and shape, or for constant grain size (a sieve fraction) and density, or for constant grain size (a sieve fraction) and shape;
• logarithmic grain density, valid for constant grain size (a sieve fraction) and shape;
• logarithmic grain shape, valid for constant grain size (a sieve fraction) and density;

Distributions of other variables than those of the PSI-sedimentation velocity and of the PHI-grain size, such as those of  Reynolds' number (laboratory, standard, and local), grain density, grain shape, may be suitable for certain applications.

Appendix

Logarithmic notations of grain size (PHI) and sedimentation velocity (PSI)

Retaining the geometric grade scale of J. A. Udden (1898), W. C. Krumbein (1934) introduced binary logarithm of grain size, PHI (transcription of the Greek letter Ø). This notation became popular among geologists because it makes calculations and mathematical expressions easy.

Similarly, G. V. Middleton (1967) applied the binary logarithm to sedimentation velocity, and defined PSI (transcription of the Greek letter ).

The pertinent relations are as follows:

PHI = -log₂Xi

X_i = 2^-PHI

PSI = -log₂Y_i

Y_i = 2^-PSI

Explanation:

X₁ is a dimensionless ratio of a given grain size, d_i, in millimeter, to the standard grain size of 1 millimeter, d₀ (D. A. McManus, 1963, W. C. Krumbein, 1964):

X_i = d₁/d₀

Y_i is a dimensionless ratio of a given sedimentation velocity, v_i, in centimeter per second, to the standard sedimentation velocity of 1 centimeter per second, v₀:

Y_i = v₁/v₀

Shape Factor (J. Brezina, 1979b)

From various definitions of grain shape, the simple flatness characteristics, the ratio of the grain height to its average perpendicular dimension, is the hydrodynamically most effective one (A. T. Corey, 1949, and independently McNown & Malaika, 1950). This dimensionless ratio number relates the minimum, medium and maximum mutually perpendicular grain dimensions, a, b, c respectively:

SF = a/(b*c)^0.5

The SF value for isometric shape, such as cube (with its plane normal to the direction of motion), is, by theory, the same as for the smooth sphere, i. e. 

SF_iso = 1.0.

However, the hydrodynamic roughness of the isometric particles causes their drag coefficient greater than that of the smooth spheres. This results into the higher SF value for spheres than is mathematically possible. The author calls the Shape Factor resulting from the drag coefficient the Hydraulic Shape Factor, SF' (J. Brezina, 1979b, p. 2 - 3). In order to retain his drag coefficient equation (J. Brezina, 1979b, p. 5) valid for geometric SF, he adjusted the equation parameters such that the smooth spheres with SF' value 1.18 correspond to the smaller drag coefficient:

SF'_sph = 1.18.

The author has not studied the influence of  roughness on drag coefficient of grains with lower SF values. However, he assumes that the grain smoothness may increase SF' by a value lower than 0.2, similar to the smoothing isometric grains into spheres.

The naturally worn irregular grains have the shape factor values in the relatively narrow range of  (Byrnon C. Colby + Russell P. Christensen, 1957; E. F. Schulz, R. H. Wilde, & M. L. Albertson, 1954)

SF'_irr = 0.65 ± 0.05.

However, most authors take the grain shape of the smooth sphere as a reference shape, irrespective which shape the grains really have. This is in conflict with the reality excused only by the unavailability (and difficulty) of grain shape measurement. This is as if a 'physicist says about the horse: let's assume it is a sphere!' (J. Brezina, 1992, p. 166; Miroslaw Jonasz, 1991, p. 147). Taking the smooth sphere instead of the rotational  ellipsoid with SF' = 0.65 as reference causes enormous size reduction of the irregular grains (J. Brezina, 1979b, p. 2).

Return to Home.

You are visitor number since July 17, 2000